4.10.3 El plano complejo como modo algebraico

El punto clave es usar, como modelo para el plano, el plano complejo, véase sección 4.2. Podemos pensar que los dos puntos dados son los números 0 y 1. ¿Qué otros números del plano complejo se pueden construir a partir de estos dos? A continuación, veremos que el conjunto de puntos 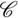que se puede construir forma —visto como números complejos— un campo, es decir, los números en  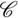se pueden sumar, restar, multiplicar y dividir. Antes de ello, observemos que se pueden construir perpendiculares con regla y compás si damos un punto P  y una recta ℓ, pues se debe construir la perpendicular k a  ℓ que pasa por P.

Como la figura 4.64 sugiere, hay que distinguir el caso en que P  pertenece a ℓ del caso en que no pertenece. La figura indica los cuatro pasos en ambos casos.

También podemos construir paralelas: la paralela a la recta ℓ que pasa por P se obtiene al construir la perpendicular a k  que pasa por P, donde k es la perpendicular a ℓ que pasa por P . Por la interpretación geométrica de la suma de números complejos (véase sección 4.9.2), es posible construir el número  x + y si ya se tienen construidos x, y con anterioridad: ahora sólo necesitamos intersecar la paralela a 0y por x con la paralela a 0x por y. En otras palabras, si x, y pertenecen a 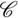, entonces también  x+  y lo hará.

Figura 4.64 Indicación de cómo construir perpendiculares. A la izquierda para puntos P fuera y a la derecha para puntos P  sobre la recta ℓ.

Por otro lado, podemos construir –x si ya está construido x, dado que –x es simplemente el reflejo de x en el punto 0. Consecuentemente, si x, y pertencen a , entonces también –y  y, por lo tanto, también x-y = x + (-y).

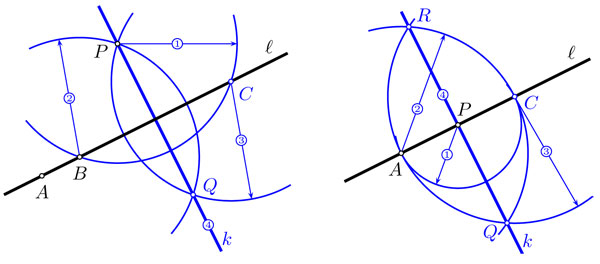
Antes de revisar la multiplicación, analicemos el compás como herramienta. Un compás puede levantarse de la hoja de papel y, sin cambiar su apertura, trazar una circunferencia en otro lugar con el mismo radio. Parece que el compás es una herramienta más poderosa de lo que pensábamos —que, simplemente, construir rectas y circunferencias a partir de puntos ya construidos—. Pero no es así: podemos usar solamente rectas y circunferencias para implementar toda la funcionalidad del compás, como lo muestra la figura 4.65 a la izquierda.

4.65 Indicaciones de cómo transportar distancias y ángulos de un lugar a otro sin el uso del compás.

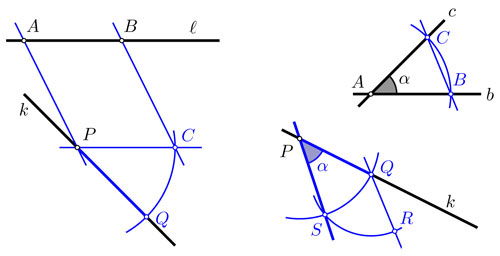
En esta figura se transportó la distancia entre los puntos A y B a la recta k, partiendo del punto dado P. Como resultado, se obtiene el punto Q sobre k, que está a la misma distancia que B de A. Del lado derecho se muestra cómo se pueden transportar ángulos. Si se quiere transportar el ángulo α entre dos rectas b y c, al punto P a partir de la recta k, entonces, primero se construye el punto Q —al transportar la distancia AC a P —, luego el punto R—al transportar la distancia CB a una paralela a BC por Q — y, finalmente, se interseca la circunferencia con centro P que pasa por Q con la circunferencia con centro Q que pasa por R, para obtener el punto S y  .

Claro es que los números enteros son construibles si se transporta, por ejemplo, el segmento s con extremos 0 y 1 a la derecha de 1, para encontrar el punto 2. Luego se transporta s a la derecha de 2, para obtener 3.

 Veamos ahora la multiplicación. Según la interpretación geométrica que se observa en la figura 4.66, debemos sumar los ángulos y multiplicar los valores absolutos. Ambas cosas son bastante fáciles de lograr con regla y compás: los ángulos se suman con el método para transportar explicado arriba y el producto de los valores absolutos se obtiene por semejanza, como en la figura 4.67.

A continuación, veamos la última de las cuatro operaciones básicas: la división. Como en la resta, es suficiente mostrar que podemos construir con regla y compás el inverso multiplicativo de un número construible z dado. Con tal fin usamos la representación geométrica: debemos construir el negativo del ángulo de z y el inverso multiplicativo 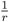, de su valor absoluto r. Esto se hace de nuevo por semejanza, como lo indica la figura 4.67.

Como consecuencia, podemos construir todos los números racionales, es decir, , si 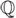denota al conjunto de los números racionales.

4.66 Construcción para encontrar el producto r s de dos números reales r y s positivos.

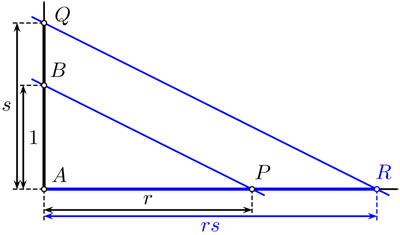
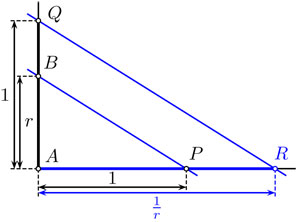
4.67 Construcción para encontrar el inverso multiplicativo 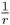de un números real r positivo.

Por último, observemos que si un número complejo z es construible, entonces también lo serán sus dos raíces cuadradas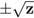; este hecho se suele abreviar diciendo que los números construibles son "cerrados bajo la operación de sacar la raíz cuadrada". Otra vez recurrimos a la interpretación geométrica de sacar raíces, según lo hicimos en la figura 4.67. Debemos dividir el ángulo de z en dos —que es fácil con regla y compás— y obtener la raíz cuadrada del valor absoluto de z, como se indica en la figura 4.68.

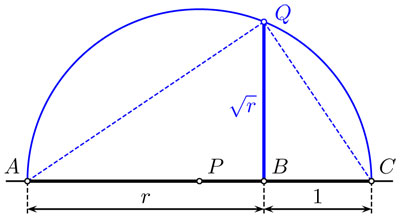
4.68 Construcción para encontrar la raíz cuadrada 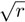de un número real r positivo.

En efecto, por semejanza de los triángulos 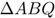y 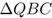, sigue que la altura x =BQ debe satisfacer x : r = 1 : x, es decir,  x² = r y por ello 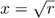. Con ello, hemos llegado al primer resultado importante de esta sección:

 Teorema 1: Los números construibles 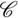forman un campo que es cerrado bajo la operación de sacar raíces cuadradas.

---